Deutsch-Jozsa, Simon's Algorithms

Table of Contents

1. Deutsch-Jozsa Algorithm
2. Simon's Algorithm

Deutsch-Jozsa Algorithm

The Deutsch-Jozsa algorithm is different than the other algorithms we talked about in the last lesson. It has an exponential advantage over the best known classical algorithm.¹ Specifically, the best classical algorithm to solve the problem is $O(2^n)$, while our formulation of the Deutsch-Jozsa algorithm runs in $O(1)$. A huge difference!

The problem is formulated as follows: suppose we have some boolean function $f(x)$ that takes in some bitstring $x$ and returns either a $0$ or a $1$. This function will be either constant or balanced. A function is constant if $f(x)=f(y)$ for all $x,y$. A function is balanced if an equal number of inputs produce $0$ and $1$ as their outputs. The problem states that given a black-box function $f$ (i.e. a function that we don't have access to the inner workings of) that is either constant or balanced, figure out whether it is constant or balanced.

How do we figure out the best algorithm that this problem classically? Well, it turns out to be pretty intuitive. We know that either half of the $2^n$ inputs will output the same result or all of them will. So we need to check one more than half, or $2^{n-1}+1$, in the worst case to conclusively figure out which it is. There is no better approach to solve this; it runs in $O(2^n)$.

The key to coming up with our quantum algorithm is figuring out what form to express $f(x)$ in. What we really want is a function that takes in a quantum state and returns the same state but with some distinguishable marking based on whether $f(x)=0$ or $1$.

This is a situation where a phase change becomes really useful! We will use a really common tool in quantum computing known as an oracle, in particular a phase oracle, which we define as follows:

The other tool we will use is the Hadamard transform (usually notated as $H^{\otimes n}$), which is simply the application of a Hadamard gate on each qubit, placing a quantum state $|\psi\rangle$ into equal superposition from $|0\rangle$ to $|2^n-1\rangle$.

In formal notation, we can write the Hadamard transform as

Once we have these tools, assembling the algorithm is simple. We simply start at $|0^n\rangle$ and append a Hadamard transform to each side of the oracle:

where $j \cdot k$ can be thought of as the bitwise inner product mod 2, or the parity of the bitwise AND of $j$ and $k$.

Now let's say that $|k\rangle = |0\rangle$. This leaves us with the amplitude

and recall that the probability of measuring a quantum state is the square of its amplitude. The key observation is that we can guarantee whether $f(x)$ is constant or balanced based on the amplitude of $|0\rangle$!

Think through what will happen if $f(x)$ is constant as well. You should be able to realize that looking at the amplitude of $|0\rangle$, and therefore the probability of measuring it, will tell us with certainty whether $f(x)$ is constant or balanced.

It may not seem obvious how to measure the time complexity of an algorithm like this. In this algorithm, we call the oracle once, and we use a linear number of gates due to the Hadamard transform. This is somewhat analogous to the computer science concepts of time complexity and space complexity, but more often in quantum computing, we categorize algorithms based on how they compare to classical algorithms. For the Deutsch-Jozsa algorithm, it would be more useful to just say that it has an exponential speedup over its classical counterpart.

Now, let's try implementing this in Qiskit together, because I think it teaches an important lesson.

Qiskit has a great built-in object called PhaseOracle that takes in a boolean expression as a string. Note that the number of inputs to the boolean should be equal to the number of qubits the oracle is applied to.

I have written two example boolean expressions, one corresponding to a constant function (always 0) and the other corresponding to a balanced function (simply returns the parity of the input).

ex_constant = '(a & ~a) | (b & ~b) | (c & ~c) | (d & ~d)'
ex_balanced = '(a ^ b) ^ (c ^ d)'

Let's test out the balanced function. The code for our circuit is as follows:

from qiskit import QuantumCircuit
from qiskit.circuit.library import PhaseOracle

n = 4
qc = QuantumCircuit(n)
for i in range(n):
    qc.h(i)
oracle = PhaseOracle(ex_balanced)
qc.append(oracle, qc.qubits)
for i in range(n):
    qc.h(i)
qc.measure_all()
qc.draw()

Note the difference between the PhaseOracle and the other gates we apply. The oracle is not a function of qc, but rather another object that we need to import from Qiskit's circuit library. This means that we apply it with the general append function. We also need to select which qubits to apply it to; qc.qubits will simply select all of them, which is what we want here.

I have arbitrarily chosen to test our circuit on 4 qubits, but you can set n to whatever you want. The code block above results in the following output:

        ┌───┐┌───────────────┐┌───┐ ░ ┌─┐         
   q_0: ┤ H ├┤0              ├┤ H ├─░─┤M├─────────
        ├───┤│               │├───┤ ░ └╥┘┌─┐      
   q_1: ┤ H ├┤1              ├┤ H ├─░──╫─┤M├──────
        ├───┤│  Phase Oracle │├───┤ ░  ║ └╥┘┌─┐   
   q_2: ┤ H ├┤2              ├┤ H ├─░──╫──╫─┤M├───
        ├───┤│               │├───┤ ░  ║  ║ └╥┘┌─┐
   q_3: ┤ H ├┤3              ├┤ H ├─░──╫──╫──╫─┤M├
        └───┘└───────────────┘└───┘ ░  ║  ║  ║ └╥┘
meas: 4/═══════════════════════════════╩══╩══╩══╩═
                                       0  1  2  3 

This looks different from anything we've seen before! The PhaseOracle looks like a gate, but it spans all of the qubits instead of just one of two. In truth, it makes more sense to think of the oracle as an operator, more akin to a black-box function with a bunch of gates inside it.

The important thing you need to know is that the PhaseOracle object is a "composed" wrapper for all of these gates, which would really clutter up the circuit. But when we want to simulate the circuit, we need to decompose it first.

There are two ways to do this. The first is adding a pretty self-explanatory line of code before simulating:

qc = qc.decompose()

However, I don't recommend this because this decompose function may not fully decompose the circuit. If other abstract gates are used within the abstract gate you're decomposing, it doesn't necessarily decompose those with one function call. You can fix this by calling the decompose method several times, but that's pretty clunky.

The way I prefer, if you know the backend you'll be simulating on, is to use the transpile function:

from qiskit_aer import AerSimulator

qc = transpile(qc, backend=AerSimulator())

This will decompose the circuit into specifically the gates that your backend can handle.² You don't have to worry about how this works in detail too much for the purposes of this course. You can always use the AerSimulator as your backend in all of the algorithms we will work on, and transpile to it accordingly.

With our transpilation complete, we can finally get the output of our simulation.

{'1111': 2048}

Since $|0\rangle$ never appears, we know that its amplitude is $0$ and our input function is balanced.

The Deutsch-Jozsa algorithm is really cool, but think about how you would actually solve this problem. You would probably test out a handful of different input values of the function $f(x)$. The moment you get a second unique value, you know the function is balanced. If that doesn't happen after, say, 20 or 30 queries, you can be pretty confident that the function is constant.

Even though the classical approach above does not work with certainty, it doesn't really feel like the Deutsch-Jozsa algorithm is all that powerful, even if it is $O(1)$. Can we do better?

Simon's Algorithm

Simon's algorithm is a really important algorithm because it provides the most compelling case so far that quantum computers can be more powerful than classical computers.

The best classical approach to solve Simon's problem is $O(2^{n/2})$, while the best quantum approach offers an exponential speedup. While this speedup is more humble than the Deutsch-Jozsa algorithm, the difference is that you cannot solve the algorithm probabilistically with much confidence until you reach exponential time either.

The other factor to note about the runtime before we begin is that the algorithm has both quantum and classical elements: the quantum element is only $O(n)$, but a polynomial classical post-processing is required to actually get the answer.

Let's formulate the problem. We are given some function $f(x)$ with the property that if $f(x)=f(y)$ for two binary strings $x \neq y$ of length $n$, then $x \oplus y = s$, where $s$ is some secret binary string. The problem tasks us to find $s$ given $f(x)$.

This doesn't seem that easy to solve. We will need to guess values and gain information based on what we guess. In the best case, on query $j$, we'll eliminate at most $j-1$ possibilities for $s$. To find $s$ with certainty, we'd need to eliminate $2^{n}-1$ possibilities, which takes about $2^{(n+1)/2}$ queries. This turns out to be the best classical approach. It turns out that probabilistic algorithms can't get us a consistent result in polynomial time either.

Now let's think about how to solve it using a quantum computer. We want to assemble an oracle $O_f$, but we need to convey more than a single marking here. We really want to have access to the entire output of $f(x)$, so a phase oracle won't work here.

It would be great if we could map a quantum state $|z\rangle \mapsto |f(x)\rangle$ using $O_f$, where $|x\rangle$ is some other quantum state. However, remember that a quantum operator, like our oracle, must be reversible, so $O_f(O_f|x\rangle) = |x\rangle$.³ It turns out that the easiest way to do this is by having $O_f$ map $|z\rangle \mapsto |z \oplus f(x)\rangle$, since $(z \oplus f(x)) \oplus f(x) = z$.

We will compute $f(x)$ in a different register, so $O_f$ will be defined as

In contrast to our phase oracle from before, this is known as a bit oracle.⁴

Let's now write out the algorithm. I will use a pretty common piece of notation I haven't used before, which is using calligraphic letter subscripts to notate different quantum registers. This notation is useful when you want to be explicit about what register certain operations will apply to, which will be particularly important here.

We will start in state $|0^n\rangle_\mathcal{A} |0^n\rangle_\mathcal{B}$, with $n$ qubits in register $\mathcal{A}$ and $n$ qubits in register $\mathcal{B}$. We will then apply $H_\mathcal{A}^{\otimes n}$ to the state, a Hadamard transform on register $\mathcal{A}$. We will then apply $O_f$, which leaves the value of register $\mathcal{A}$ unchanged and sets register $\mathcal{B}$ to $f(H^{\otimes n}|0\rangle_\mathcal{A})$. We then apply $H_\mathcal{A}^{\otimes n}$ to the state again and measure the value in register $\mathcal{A}$. We can just discard the value in register $\mathcal{B}$.

If you're being observant, you'll notice that something seems very odd about my description above. We are applying the oracle, which only seems to change the state of register $\mathcal{B}$, but then never use or measure its state again. Why can't we just remove the oracle? Well, in that case, it would just be two Hadamard transforms applied on register $\mathcal{A}$ cancelling each other out, so clearly something must be going on.

I want to convince you that register $\mathcal{A}$ is being affected by the application of the oracle, even if its state isn't changed. This is an extremely important and foundational principle in quantum mechanics known as back action.⁵

To understand this phenomenon, let's take a look at a much simpler quantum circuit; instead of our bit oracle, we will just use a $CX$ gate.

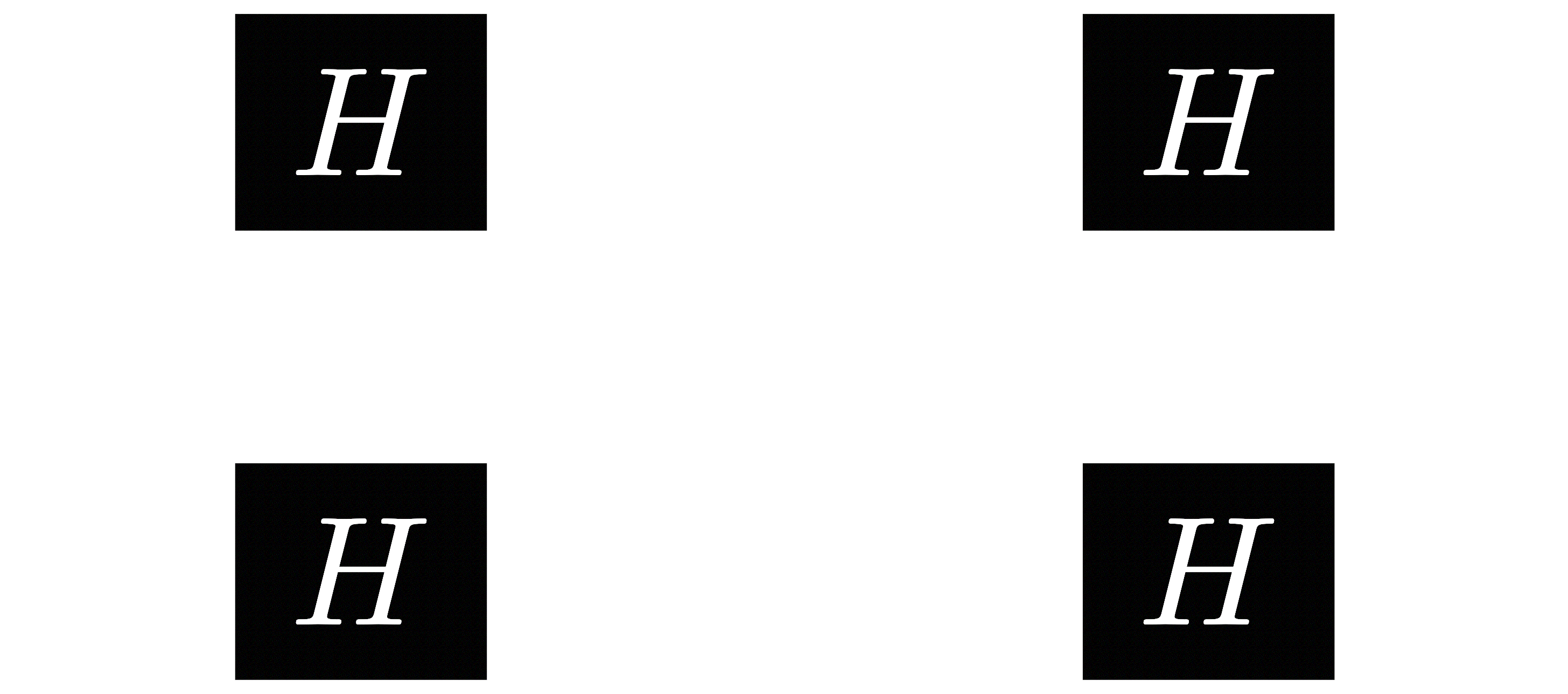
Let's first just look at the gates on the bottom wire, $HXH$, ignoring the top wire. If you do the matrix multiplication, you'll find that $HXH=Z$, a fact that will be really useful for us here.

Hence, we can rewrite our circuit as the following:

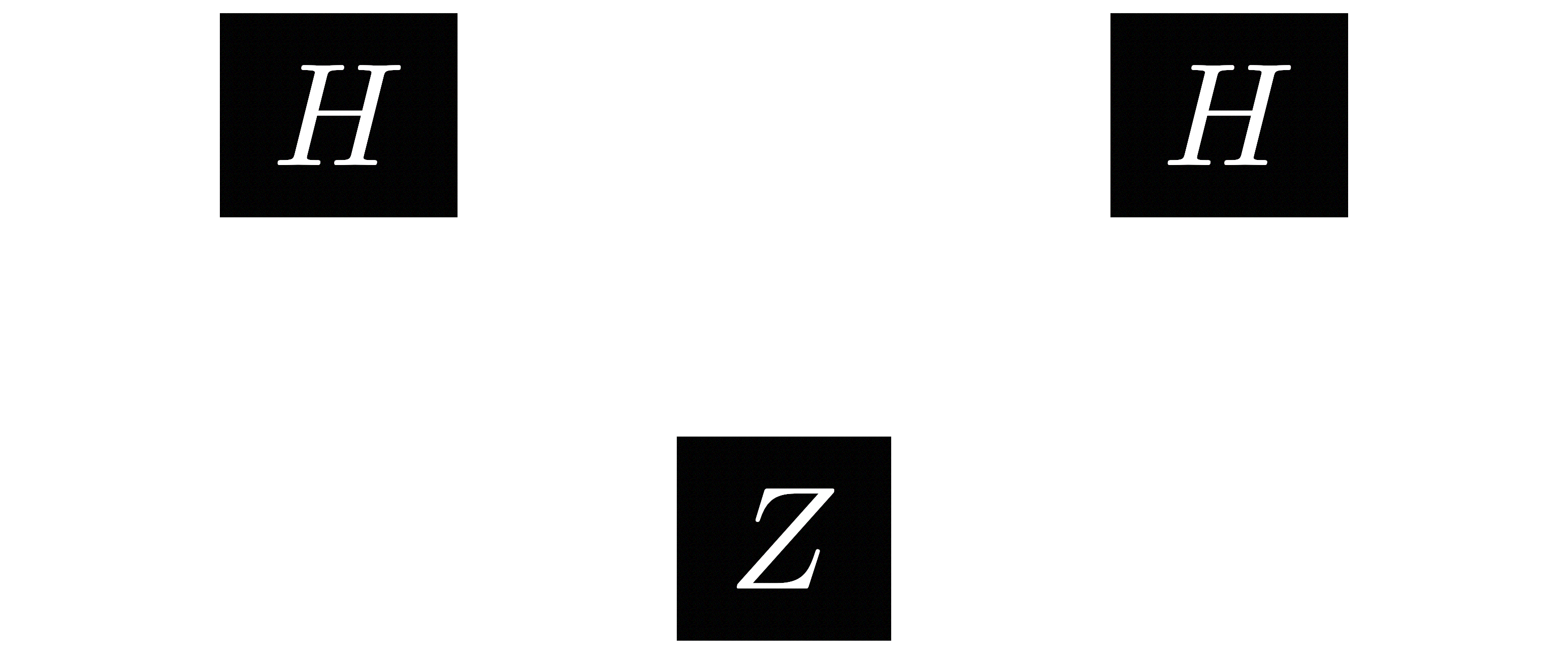
The next key observation is a lot more subtle. Remember that the control qubit must be $|1\rangle$ for the $Z$ gate to be applied on the target qubit. But remember that the $Z$ gate doesn't affect the qubit it is being applied to if it is $|0\rangle$ and performs a phase flip if it is $|1\rangle$. That means that the state is not changed as a result of the $CZ$ gate unless it is $|11\rangle$.

This means that the effect of the gate is symmetrical, and we can switch the control and target qubits! Hence, we are left with this circuit:

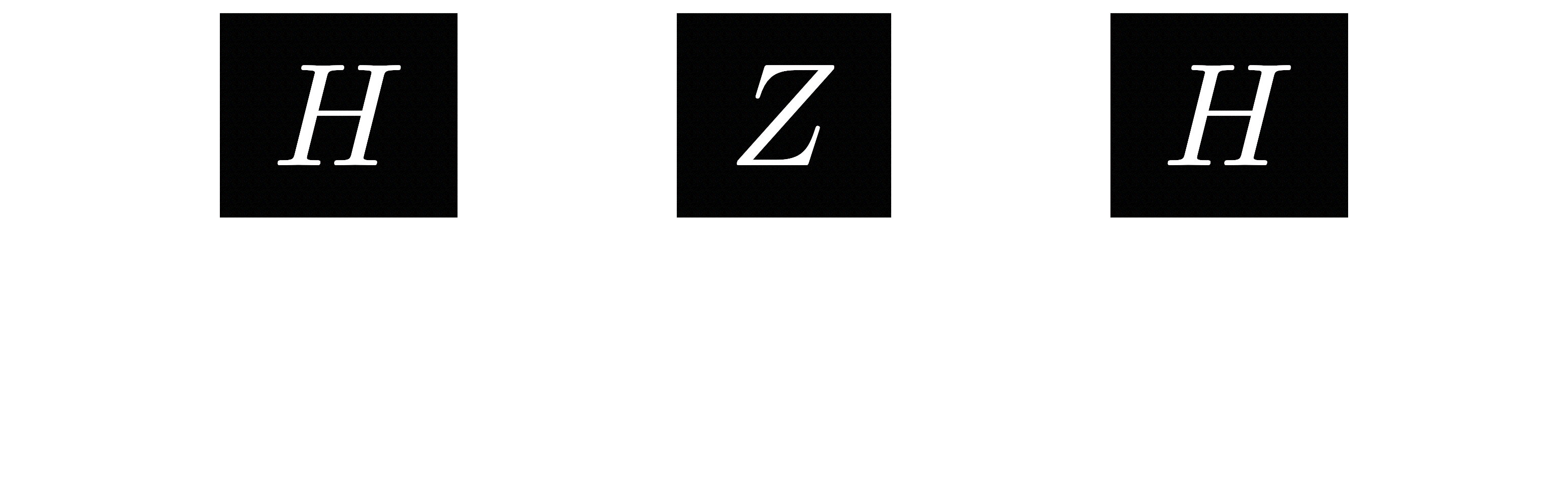
But since, as we mentioned before, $HZH=X$, we can simplify this further to

or a reversed $CX$ gate. Hence, applying a Hadamard transform before and after a $CX$ gate will reverse the control and target qubits!

I think it's hard to really internalize this fact without an example. Let's say that we have the state $|01\rangle$ and let's try to compute each of the two circuits.

Let's start with the reversed $CX$ gate first. Since the control qubit is $|1\rangle$ and the target qubit is $|0\rangle$, the resulting state will be $|11\rangle$. That's easy enough.

Now, let's look at the original state we had, where Hadamard transforms surrounded the $CX$ gate. We know that the first Hadamard transform will result in

and the $CX$ gate will flip the $|10\rangle$ and $|11\rangle$ states, resulting in

which can be factored as $|-\rangle|-\rangle$. When the Hadamard transform is applied again, this results in $|11\rangle$ as our final state. Hence, the control qubit was flipped for this input while the target qubit was unchanged, resulting in exactly the same output as the reversed $CX$ gate!

It's really important to note that in the example above, the state of the control qubit was not actually changed, but the effect of the change on the target qubit from the $CX$ gate actually ended up changing the control qubit due to the setup of the states going into the $CX$. It's really subtle and tricky to understand! But it gives us a stronger intuition for why our bit oracle still has an effect despite not applying to the register we measure.

Now, let's look at the quantum state more closely. After the second Hadamard transform, we are left with

Now let's find the probability of seeing some value $|k\rangle$ when we measure register $\mathcal{A}$. This is easier if we start by finding the probability of seeing a specific pair $|k\rangle_\mathcal{A}|f(j)\rangle_\mathcal{B}$. The only two values that would produce $f(j)$ are $j$ and $j \oplus s$, so the amplitude of each pair would be

The algebraic manipulation here uses the distributive property of the XOR operation. We can see that this amplitude is $0$ if $s \cdot k = 1$ and $1/2^{n-1}$ if $s \cdot k = 0$. Hence, the probability of seeing $|k\rangle$ if $s \cdot k = 1$ is $1/2^{2n-2}$.

It may be subtle to see how this helps us. We know that if $s \cdot k = 0$, then $s$ and $k$ are perpendicular if we think of them as $n$-dimensional vectors. If we had $n-1$ linearly independent vectors perpendicular to $s$, then we could pretty easily find the vector perpendicular to all of them (by the properties of linear algebra, there can only be one), which will be $s$. We also know that any term we measure will have $s \cdot k = 0$, since otherwise its amplitude would be $0$.

This means that every term we measure for a given value of $j$ is a candidate to be one of these $n-1$ vectors. We just need to confirm that each candidate is linearly independent to every other vector we have found up to that point. We can achieve this by creating a matrix of the vectors we have found so far as well as the candidate $c$ and confirming that the matrix is still full rank.

This requires sampling a subset of the $2^n$ values of $j$ until we find the $n-1$ linearly independent vectors. It turns out that we can do this in $O(n)$ with very high confidence. Once we have that, we know that

since the inner product of $s$ with all of the vectors must be $0$. And we are done!

It's important to note that only the process of querying the oracle is quantum here. The rest is simply classical techniques you would cover in a linear algebra class. It's also important to mention that the specific runtime of Simon's algorithm would depend on the classical postprocessing. For example, I think the version I've presented is $O(n^4)$ since we would have to perform row reduction (which is $O(k^3)$ for $k$ vectors) $n$ times.

In most computer science contexts, this would be pretty bad. But in quantum computing, since we're often looking at algorithms that have exponential classical runtime, we don't really care about what the specific polynomial runtime is. We're more interested in the runtime of the quantum part. For problems that involve querying an oracle, like this one, that's known as the query complexity. The query complexity of Simon's algorithm is unambiguously $O(n)$.

And that's it! I hope you're a little more convinced that quantum computers can provide really powerful speedups in the right context. However, in truth, not many algorithms offer an exponential speedup. It is an area of active research to find more quantum algorithms that offer large speedups over classical algorithms.

I'm not going to code Simon's problem on Qiskit, as I want to leave it as an exercise for you to try. I highly recommend using Qiskit's BitFlipOracleGate, and using NumPy for the classical postprocessing operations.

1. The exponential speedup of the Deutsch-Jozsa algorithm only exists if we insist that the algorithm be deterministic. It turns out that the best classical probabilistic algorithm can run in $O(k)$ with $1-1/2^k$ probability of success, a pretty major difference. However, it is not a deterministic, constant approach like the quantum algorithm.

2. Different models of IBM quantum hardware may use different sets of gates, which correspond to physical circuitry on the quantum chip. This concern is relatively unique for quantum computing, due to how many different possible ways there are to construct quantum computers. Qiskit tries to make it easy to transpile your circuit to whatever backend you are using as long as you know which one you want to use.

3. I didn't really focus on it for the phase oracle, but when you just need a "marker" or boolean indicator, that's why flipping the phase works so well. Go back to the phase oracle and make sure to convince yourself that it really is always reversible.

4. It turns out that phase oracles and bit oracles are equivalent. It just makes more sense to present one over the other in different scenarios. I wanted to make sure that you have a good taste of both in this lesson.

5. Although his notes are a source I draw from a lot throughout these lessons, I want to particularly highlight Peter Shor's lecture notes on Simon's algorithm. Reading these for the first time actually made me understand back action occurs in quantum computing, which had been extremely confusing for me in the past.